반응형
Hypothesis
- 인공신경망을 나타냄
EX) Linear Regression - W와 b라는 변수를 학습해서 주어진 데이터에 최적화함
![]()
(이미지출처: boostcourse ai tech pre course)
Simpler Hypothesis Function
- 이번엔 Bias를 제거한 H(x) = Wx 로 실험해보자
- 아래와 같은 데이터가 존재할 때
| Hour(x) | Points(y) |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
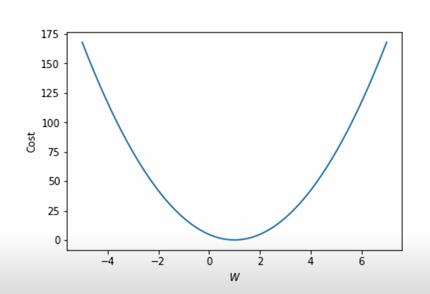
(이미지출처: boostcourse ai tech pre course)
- CostFunction: 모델의 예측값이 실제값과 얼마나 다른지 나타냄, 좋은모델일수록 낮은값을 가짐
- Linear Regression에서 사용되는 Costfunction은 MSE(Mean Squared Error)를 사용
- CostFunction을 최소화 하기 위해
- 기울기가 음수일 경우에는 W가 커져야하며 양수일 경우에는 W가 작아져야함
- 기울기가 가파를수록 Cost가 큰것이니 W를 크게바꾸고 평평할수록 Cost가 작은것이니 W를 작게바꿔야함
import torch
x_train = torch.FloatTensor([[1],[2],[3]])
y_train = torch.FloatTensor([[1],[2],[3]])
w = torch.zeros(1, requires_grad=True)
optimizer = torch.optim.SGD([w], lr=0.15)
nb_epochs = 10
for epoch in range(nb_epochs+1):
hypothesis = x_train * w
cost = torch.mean((hypothesis - y_train) ** 2)
print(f'EPOCH {epoch}, W:{w}, cost:{cost}')
optimizer.zero_grad()
cost.backward()
optimizer.step()
->
EPOCH 0, W:tensor([0.], requires_grad=True), cost:4.666666507720947
EPOCH 1, W:tensor([1.4000], requires_grad=True), cost:0.7466669678688049
EPOCH 2, W:tensor([0.8400], requires_grad=True), cost:0.11946680396795273
EPOCH 3, W:tensor([1.0640], requires_grad=True), cost:0.0191146582365036
EPOCH 4, W:tensor([0.9744], requires_grad=True), cost:0.00305833644233644
EPOCH 5, W:tensor([1.0102], requires_grad=True), cost:0.0004893290461041033
EPOCH 6, W:tensor([0.9959], requires_grad=True), cost:7.829209789633751e-05
EPOCH 7, W:tensor([1.0016], requires_grad=True), cost:1.2527179023891222e-05
EPOCH 8, W:tensor([0.9993], requires_grad=True), cost:2.0041973129991675e-06
EPOCH 9, W:tensor([1.0003], requires_grad=True), cost:3.206215808404522e-07
EPOCH 10, W:tensor([0.9999], requires_grad=True), cost:5.128529423359396e-08- 점점 작아지는 Cost와 1에 수렴하는 W를 확인할 수 있음
- 학습가능한 변수들과 lr을 통해 optimizer를 선언
- cost를 계산한 후 gradient descent를 실행
- optimizer w를 gradient에 저장한후 w의 값을 gradient에 맞게 업데이트함
- optimizer.zero_grad() -> optimizer에 저장되어있는 모든 학습가능한 변수의 gradient를 0으로 초기화함
- cost.backward() -> cost function을 미분해서 각 변수들의 gradient를 채움
- optimizer.step() -> 저장된 gradient값으로 gradient descent를 실행
반응형
'부스트캠프 AI Tech 2기 > Precourse' 카테고리의 다른 글
| Minibatch Gradient Descent (0) | 2021.08.01 |
|---|---|
| Multivariate Linear Regression (0) | 2021.08.01 |
| Linear Regression (0) | 2021.07.29 |
| Tensor Manipulation 2 (0) | 2021.07.29 |
| Tensor Manipulation 1 (0) | 2021.07.28 |
반응형
Hypothesis
- 인공신경망을 나타냄
EX) Linear Regression - W와 b라는 변수를 학습해서 주어진 데이터에 최적화함

(이미지출처: boostcourse ai tech pre course)
Simpler Hypothesis Function
- 이번엔 Bias를 제거한 H(x) = Wx 로 실험해보자
- 아래와 같은 데이터가 존재할 때
| Hour(x) | Points(y) |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |

(이미지출처: boostcourse ai tech pre course)
- CostFunction: 모델의 예측값이 실제값과 얼마나 다른지 나타냄, 좋은모델일수록 낮은값을 가짐
- Linear Regression에서 사용되는 Costfunction은 MSE(Mean Squared Error)를 사용
- CostFunction을 최소화 하기 위해
- 기울기가 음수일 경우에는 W가 커져야하며 양수일 경우에는 W가 작아져야함
- 기울기가 가파를수록 Cost가 큰것이니 W를 크게바꾸고 평평할수록 Cost가 작은것이니 W를 작게바꿔야함
import torch
x_train = torch.FloatTensor([[1],[2],[3]])
y_train = torch.FloatTensor([[1],[2],[3]])
w = torch.zeros(1, requires_grad=True)
optimizer = torch.optim.SGD([w], lr=0.15)
nb_epochs = 10
for epoch in range(nb_epochs+1):
hypothesis = x_train * w
cost = torch.mean((hypothesis - y_train) ** 2)
print(f'EPOCH {epoch}, W:{w}, cost:{cost}')
optimizer.zero_grad()
cost.backward()
optimizer.step()
->
EPOCH 0, W:tensor([0.], requires_grad=True), cost:4.666666507720947
EPOCH 1, W:tensor([1.4000], requires_grad=True), cost:0.7466669678688049
EPOCH 2, W:tensor([0.8400], requires_grad=True), cost:0.11946680396795273
EPOCH 3, W:tensor([1.0640], requires_grad=True), cost:0.0191146582365036
EPOCH 4, W:tensor([0.9744], requires_grad=True), cost:0.00305833644233644
EPOCH 5, W:tensor([1.0102], requires_grad=True), cost:0.0004893290461041033
EPOCH 6, W:tensor([0.9959], requires_grad=True), cost:7.829209789633751e-05
EPOCH 7, W:tensor([1.0016], requires_grad=True), cost:1.2527179023891222e-05
EPOCH 8, W:tensor([0.9993], requires_grad=True), cost:2.0041973129991675e-06
EPOCH 9, W:tensor([1.0003], requires_grad=True), cost:3.206215808404522e-07
EPOCH 10, W:tensor([0.9999], requires_grad=True), cost:5.128529423359396e-08- 점점 작아지는 Cost와 1에 수렴하는 W를 확인할 수 있음
- 학습가능한 변수들과 lr을 통해 optimizer를 선언
- cost를 계산한 후 gradient descent를 실행
- optimizer w를 gradient에 저장한후 w의 값을 gradient에 맞게 업데이트함
- optimizer.zero_grad() -> optimizer에 저장되어있는 모든 학습가능한 변수의 gradient를 0으로 초기화함
- cost.backward() -> cost function을 미분해서 각 변수들의 gradient를 채움
- optimizer.step() -> 저장된 gradient값으로 gradient descent를 실행
반응형
'부스트캠프 AI Tech 2기 > Precourse' 카테고리의 다른 글
| Minibatch Gradient Descent (0) | 2021.08.01 |
|---|---|
| Multivariate Linear Regression (0) | 2021.08.01 |
| Linear Regression (0) | 2021.07.29 |
| Tensor Manipulation 2 (0) | 2021.07.29 |
| Tensor Manipulation 1 (0) | 2021.07.28 |

