반응형
Maximum Likelyhood Estimation(MLE)
- 최대 가능도(우도) 추정
- 압정을 땅에 던졌을때 납작한부분이 바닥으로 떨어지는 (class1) 위로 떨어지는 (class2)가 존재
- 베르누이 분포
- (매 시행마다 오직 두 가지의 가능한 결과만 일어난다고 할 때, 이러한 실험을 1회 시행하여 일어난 두 가지 결과에 의해 그 값이 각각 0과 1로 결정되는 확률변수 X에 대해서

를 만족하는 확률변수 X가 따르는 확률분포를 의미하며, 이항 분포의 특수한 사례에 속한다.)
- (매 시행마다 오직 두 가지의 가능한 결과만 일어난다고 할 때, 이러한 실험을 1회 시행하여 일어난 두 가지 결과에 의해 그 값이 각각 0과 1로 결정되는 확률변수 X에 대해서
- 베르누이 분포
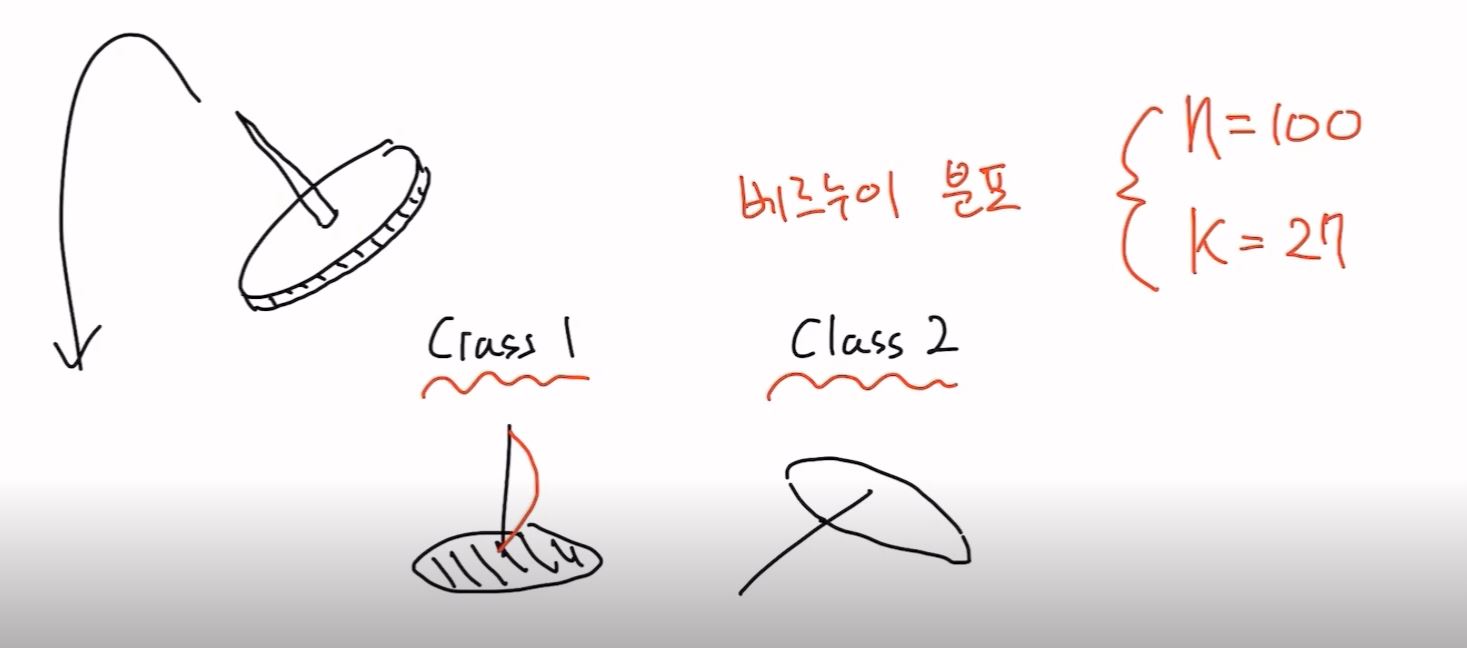
n = 100
k = 27 (class1의 횟수)
-> n,k는 observation
- 압정외 확률분포를 결정하는 쎄타를 구해야함
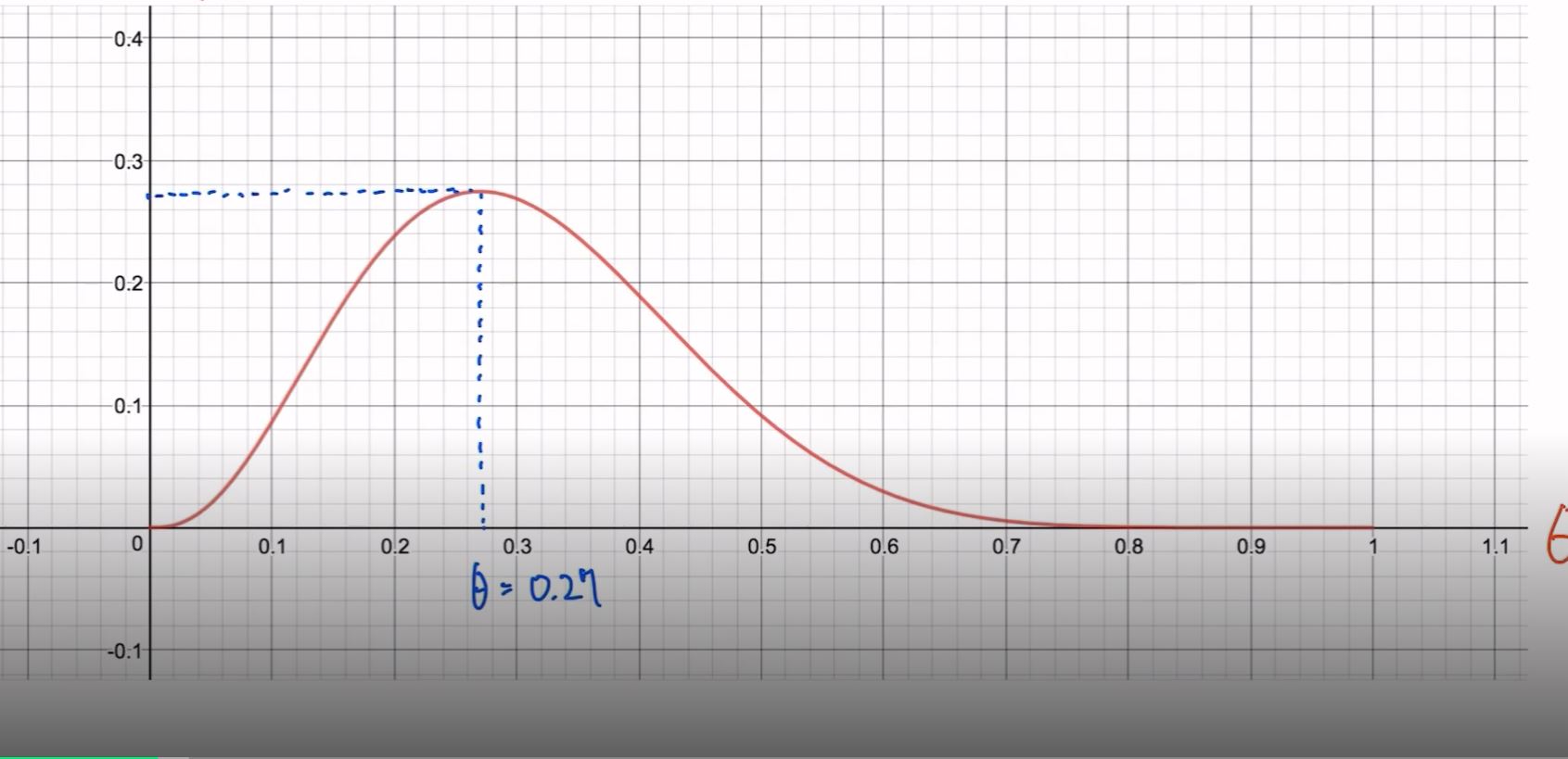
- likelyhood가 맥시멈값이 되는곳을 찾는다
- Y값이 최대가 되는 지점을 찾아보니 쎄타는 0.27이된다
- observation을 가장 잘 설명하는 어떤 확률분포 함수의 파라미터(쎄타)를 찾아내는 과정
- 지금같은 경우는 Gradient Ascent를 찾는 과정
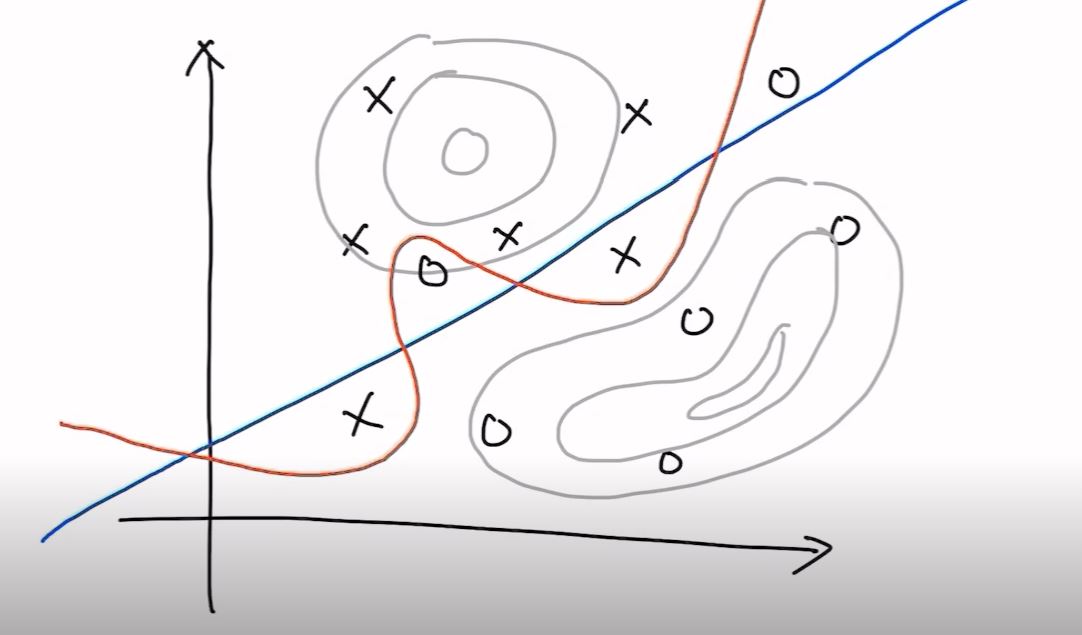
Overfitting
- MLE같은 경우에는 Overfitting이 따르게됨
- 주어진 데이터에 과하게 fitting 되어 버린 현상을 Overfitting이라함
- 파란선처럼 경계가 되어야 하지만 주어진 데이터를 가장 잘 설명하는 확률 분포 함수를 찾다보니 빨간선(Overfitting)처럼 그어짐
- Trainingset에서 MLE를 통해 과도하게 모델이 학습되지 않게 하기위해 Dev Set(Validation Set)과 Test Set을 구분하여 테스트함
- DevSet(Validation Set): 여러 모델 중에서 최종모델을 선정하기 위한 성능 평가에 관여
- TestSet: 모델의 최종 정확도 평가

- training_loss validation_loss를 통해서 학습이 얼마나 진행됐고 Overfitting 됐는지를 확인할 수 있음
- Validation_loss가 가장 낮은 지점의 epoch를 학습한 모델을 선택하여 사용

Overfitting을 막기위한 방법
- 많은 데이터를 모으자
- feature를 적게 사용하자
- ex) 사람얼굴을 설명할 때, 안경을쓰고 코가오똑하고 머리가길고 등등 여러가지 feature가 있음
- Regularization
Dropout과 BatchNormalization을 가장 많이사용함- Early Stopping
중간에(validation loss가 더이상 낮아지지 않을때) 학습을 멈춤 - Reducing Network Size
- 딥러닝에서는 Neural Network의 사이즈를 줄임
- Weight Decay
- 웨이트 파라미터의 크기를 제한
- Dropout
- BatchNormalization
- Early Stopping
LearningRate
- loss의 최저점을 찾고싶지만 알파값(learning rate)이 너무 크거나 작으면 원하는 방향으로 가지않음
- LearningRate가 너무 크면 큰폭으로 진폭해서 이곳저곳으로 튀어다님(발산)
- LearningRate가 너무 작으면 미세하게 움직이기때문에 거의 움직이지 않음
- 기본적으로 0.1을 사용해보고 학습이 너무 느리거나 발산해버린다면 LearningRate를 조절하여 최적의 LearningRate를 찾아내자
- LearningRate가 너무 클 경우

- LearningRate가 너무 작을 경우
Data PreProcessing (데이터 전처리)
- 우리가 가진 데이터가 정규분포를 따른다면 Training DataSet을 정규분포화해서 학습한다
- 아래와 같은 식으로 정규분포를 따르는 Training DataSet을 만든다

반응형
'부스트캠프 AI Tech 2기 > Precourse' 카테고리의 다른 글
| Softmax Classification (0) | 2021.08.01 |
|---|---|
| Logistic Regression (0) | 2021.08.01 |
| Minibatch Gradient Descent (0) | 2021.08.01 |
| Multivariate Linear Regression (0) | 2021.08.01 |
| Gradient Descent 심화 (0) | 2021.08.01 |
