Generative Model
우리가 만약 강아지 사진이 있다면 강아지 사진의 분산 p(x)를 예측한다
- Generation: (training set에 없는)강아지와 같은 이미지를 여러개를 생성할 수 있다 (sampling)
- Density Estimation: p(x) 어떤 이미지가 들어왔을 때 강아지같은지, 고양이같은지, 강아지가 아닌것같은지 구분해낸다 (anomaly detection - 이상행동감지)
- 이러한 모델을 explicit model이라한다.
- explicit model: 어떤 값이 주어졌을 때 확률값을 얻어낼 수 있는 모델
- implicit model: 단순히 generation만 할 수 있는모델
- Unsupervised representation learning: 귀가 있는지 등의 특성이있다.(feature learning)
Descrete Distributions
Bernoulli distribution

- 0 또는 1 (동전던져서 앞 또는 뒤)
- 이 분포를 표현하려면 1개의 숫자(parameter)가 필요하다
- 왜냐하면 앞이나올확률이 p 면 뒷면은 1-p 이기때문이다
Categorical distribution

- 6면이 나올 주사위가 있다면
- 파라미터가 5개 필요하다 왜냐하면 5개의 확률이 있다면 나머지 하나는 1 - sum(1~5)로 계산되기 때문이다
하나의 RGB컬러를 충분히 묘사하려면 256*256*256이지만 파라미터는 255*255*255개가 필요하다
즉 하나의 px에 파라미터가 255 * 255 * 255개가 필요하다.
100 * 100 px의 이미지면 255 * 255 * 255 *100 *100개의 파라미터가 필요하다. 즉 어마어마하다
mnist같은 binary 이미지에서는 2**n - 1 개의 파라미터가 필요하다.(n은 사이즈)
mnist의 possible state는 2**n 이다. (표현가능한 스테이트)
파라미터를 어떻게줄일까?
n개를 fully descributions(충분히 묘사)하지말고 쉽게할수없을까!?
n개의 px들이 모두 independent(독립적) 하다고 생각하면 어떨까?
이 때 possible state는 2**n 이고, 필요한 파라미터 수는 n개다. 왜냐하면 각각의 parameter에 대해 px한개만 있으면되기 때문
파라미터 수가 줄어서 좋지만 표현할 수 있는 이미지가 너무적다.
그렇다면 fully dependent와 independent 사이 어딘가를 찾아보자
그래서 Conditional Indenpendent 를 사용한다.
- Chain rule: x1이 independent이든 아니든 상관없이 항상 성립한다.
\begin{equation}
p\left(x_{1}, \ldots, x_{n}\right)=p\left(x_{1}\right) p\left(x_{2} \mid x_{1}\right) p\left(x_{3} \mid x_{1}, x_{2}\right) \cdots p\left(x_{n} \mid x_{1}, \cdots, x_{n-1}\right)
\end{equation} - Bayes rule:
\begin{equation}
p(x \mid y)=\frac{p(x, y)}{p(y)}=\frac{p(y \mid x) p(x)}{p(y)}
\end{equation} - Conditional independence
- z가 주어졌을 때 x와 y가 independent하다.
- independent하니까 x를 표현할 때 z가 주어지면 y는 상관이없다(지워도된다)
\begin{equation}
\text { If } x \perp y \mid z \text { , then } p(x \mid y, z)=p(x \mid z)
\end{equation}
바이너리한 이미지에 연쇄법칙을 사용한다고 가정하면 아래처럼 파라미터의 수는 2**n - 1이다.
여전히 지수승이다.

Markov assumption
Markov assumption을 적용시킴으로써 파라미터의 개수를 지수차원에서 끌어내릴 수 있다.
\begin{equation}
X_{i+1} \perp X_{1}, \ldots, X_{i-1} \mid X_{i}
\end{equation}
X_i+1은 X_i에만 dependent하고 나머지에는 independent하다(10번째 px은 9번째 px에만 dependent하고 1~8까지의 px에는 independent하다)
그렇게되면 아래와 같은 식을 얻을 수 있다.
\begin{equation}
p\left(x_{1}, \ldots, x_{n}\right)=p\left(x_{1}\right) p\left(x_{2} \mid x_{1}\right) p\left(x_{3} \mid x_{2}\right) \cdots p\left(x_{n} \mid x_{n-1}\right)
\end{equation}
이 식의 파라미터 수는 2n-1개가 필요하다.
이 conditional independency를 잘 활용하는게 Auto-regressive 모델이다.
Auto Regressive Model
- 어떻게 만들까? (parameterize p(x))
- chain rule을 써서 joint distribution을 나눈다
\begin{equation}
p\left(x_{1: 784}\right)=p\left(x_{1}\right) p\left(x_{2} \mid x_{1}\right) p\left(x_{3} \mid x_{1: 2}\right) \cdots
\end{equation}
- chain rule을 써서 joint distribution을 나눈다
Markov assumption를 통해서 i번째 픽셀이 i-1에만 dependent한것도 auto regressive 한것과 i 번째 픽셀이 1~i-1 까지의 모든 history에 dependent한것도 Auto Regressive Model이다
중요한점은 이미지 px들을 x_1 ~ x_784까지 순서를 매기는 ordering이다.
이전 n개를 고려하는건 ARN모델이라고 부른다.
이전 1개만 고려하는건 AR1모델이라고 부른다.
-> 어떤식으로 Conditional Independence를 주는지에 따라서 전체 모델의 structure가 달라진다.
Markov assumption을 주거나 어떤 임의의 conditional Independence를 주는것이 chain rule 입장에서 joint distribution을 쪼개는거에 어떤 관계가 있는지를 생각해보자
NADE(Neural Autoregressive Density Estimator)
- i번째 픽셀을 첫번째부터 i-1개의 px을 dependent하게 한다.
- 그래서 첫번째의 px에 대한 확률분포를 어느것에도 dependent하지 않은 상태로 만들고
- 두번째 px에 대한확률을 첫번째 px에만 dependent하게 만든다
( 두번째 px에 대한 확률은 첫번째 px값을 입력으로 받는 neural network를 만들어서 single scalar가 나온다음에 시그모이드를 통과하게해서 0~1로바꾼다 )
( 다섯번째 px에 대한 확률은 첫번째부터 네번째 px값을 전부 입력으로 받는 neural network를 만들어서 single scalar가 나온다음에 시그모이드를 통과하게한다 )
neural network의 입장에선 입력 차원이 계속 달라져서 weight가 계속커진다.
100번째 px에 대한 확률분포를 만들려면 99개의 입력을 받아야한다.
NADE는 explicit model이다
임의의 784개의 벡터가 입력으로 주어지면 확률을 계산할 수 있다.
n개(784)의 px이 주어지면 joint distribution을 chainrule을 통해 conditional distribution으로 쪼개고 우리의 모델이 첫번째 px에 대한 확률분포를 알고있고, 첫번재 px이 주어졌을 때 두번째 px에 대한 확률분포를 알고있다.
첫번째와 두번째가 주어졌을 때 세번째 px에 대한 확률분포를 알고있다. 그래서 각각을 independent하게 집어넣는다
\begin{equation}
p\left(x_{1}, \ldots, x_{784}\right)=p\left(x_{1}\right) p\left(x_{2} \mid x_{1}\right) \cdots p\left(x_{784} \mid x_{1: 783}\right)
\end{equation}
그렇기 때문에 generation만 하는게아니라 어떤 입력에대한 확률을 계산까지 할 수 있다.
Pixel RNN
n*n 이미지
NADE의 Denslayer와는 다르게 Recurrent neural network를 만들었다
RNN을 통해 generate를 한다.
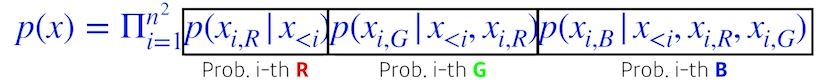
Ordering을 하는 방식에 따라 두가지로 나뉜다
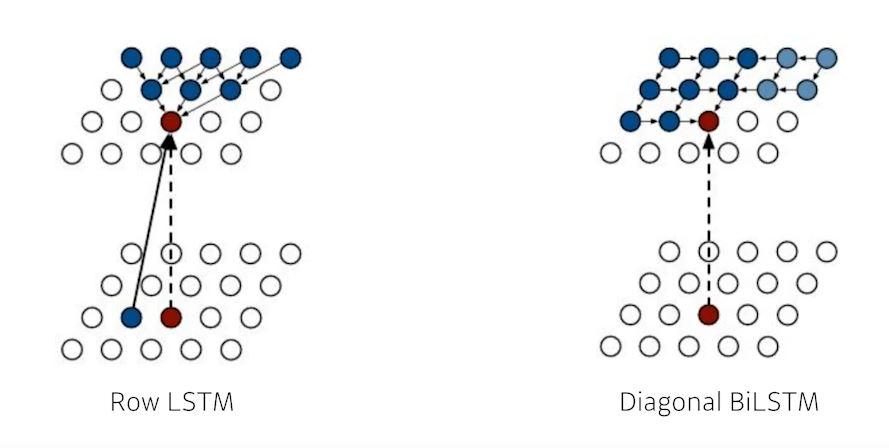
- Row LSTM
- i번째 px을 만들 때 위쪽의 정보를 활용하여 예측한다
- Diagonal BiLSTM
- 이전정보를 전부 활용한 RNN으로 px정보를 예측한다
'부스트캠프 AI Tech 2기 > 2기 U-Stage' 카테고리의 다른 글
| 2주차 Generative Models 2 (0) | 2021.08.15 |
|---|---|
| 2주차 학습정리 (0) | 2021.08.13 |
| 2주차 Transformer (0) | 2021.08.12 |
| 2주차 Sequential Model - RNN (0) | 2021.08.12 |
| 2주차 Computer Vision Application (0) | 2021.08.12 |
