부스트캠프 AI Tech 2기/2기 U-Stage
1주차 MLE(최대우도법)
모플로
2021. 8. 9. 00:59
반응형
likelihood (가능도, 우도)
- 이산 확률 분포에서는 확률 값이 가능도 이지만 연속 확률 분포에서는 확률 밀도 값이 가능도 이다.
- 우도는 딥러닝에서 주어진 데이터만으로 최적 모델 Θ(쎄타)를 찾아야한다.
- 입력값 X와 파라미터 Θ가 주어졌을때 정답 Y가 나타날 확률이다.
- 즉 지금 얻은 데이터가 이 분포로부터 나왔을 가능도를 말한다.
- 전체 표본집합의 결합확률밀도 함수를 likelihood function이라고 한다.
\begin{equation}
P(x \mid \theta)=\prod_{k=1}^{n} P\left(x_{k} \mid \theta\right)
\end{equation} - Projection을 계산하기 편하게 하위해 log를 취해준 log likelihood를 사용한다.
\begin{equation}
L(\theta \mid x)=\log P(x \mid \theta)=\sum_{i=1}^{n} \log P\left(x_{i} \mid \theta\right)
\end{equation}
MLE
- 주어진 표본에 대해 likelihood(우도)를 가장 크게 하는 모수 θ를 찾는 방법이다.
likelihood 최대화 하는 방법
- 흉내내고 싶은 데이터 분포에서 데이터를 샘플링
- 랜덤 파라미터를 가지는 모델을 이용해 확률 분포 함수를 생성 후
(가우시안 분포를 가정한다면 파라미터로 랜덤한 평균, 표준편차 설정)
(뉴럴넷의 W들도 결국 임의의 확률분포를 표현하는 파라미터라 할 수 있음 ; 뉴럴넷 == 확률분포함수) - 주어진 모델과 데이터를 이용해 확률값들을 뽑아 Likelihood를 계산하고
- 2-3 반복 후 Likelihood를 최대화하는 모델 선택
예시
아래와 같은 확률분포함수를 만든다면
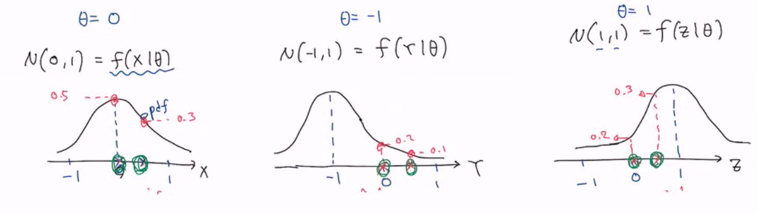
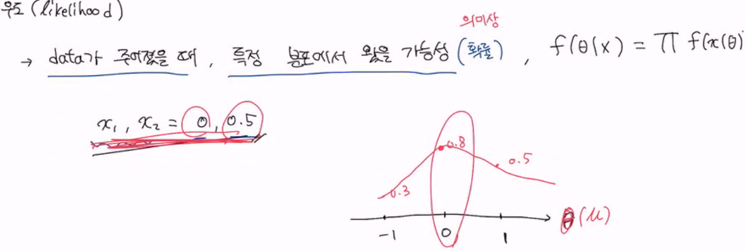
여기서 주어진 x의값을 확인했을 때, 위의 확률분포에 대입한 이후 가장 높은 쎄타가 0일때 값이 0.8이므로 MLE는 첫번째 확률분포함수가 된다.
참고
- https://aimaster.tistory.com/64 식피두님
- AI 부스트캠프 2기 이현멘토님
반응형